跳转至

Instruction Selection：指令选择

约 814 个字 6 张图片 预计阅读时间 3 分钟

这一阶段的目的很简单，就是要选择合适的机器指令来 cover 掉 IR。有两种实现：

  • Tree-oriented IR：输入是树形
  • Linear IR：输入是字符串

1. 选择方式

这里使用 Jouette 指令集架构，如图：

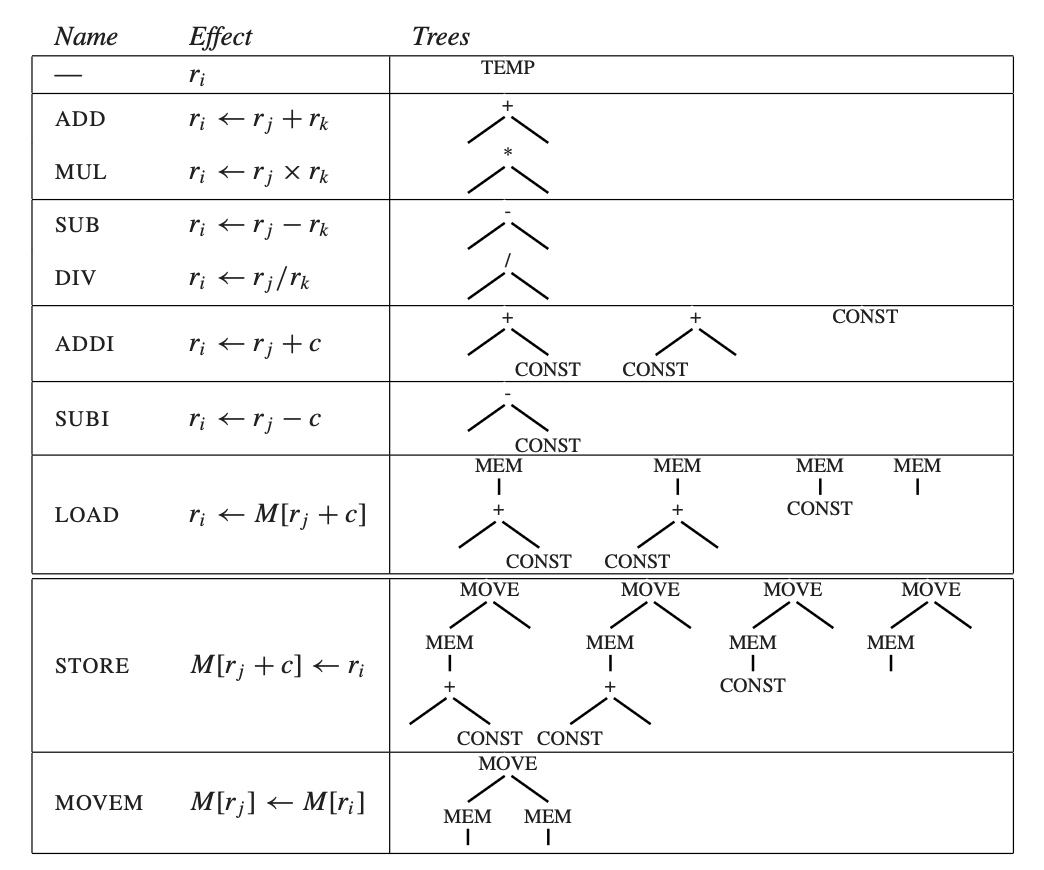
image.png

需要注意：

  • 寄存器 r0 总是零
  • 有些指令对应不止一个树形

覆盖的基本思想是把 IR 树瓦片化（tiling），也就是将 IR 树分解为多个子树，每个子树对应一个机器指令。

例子

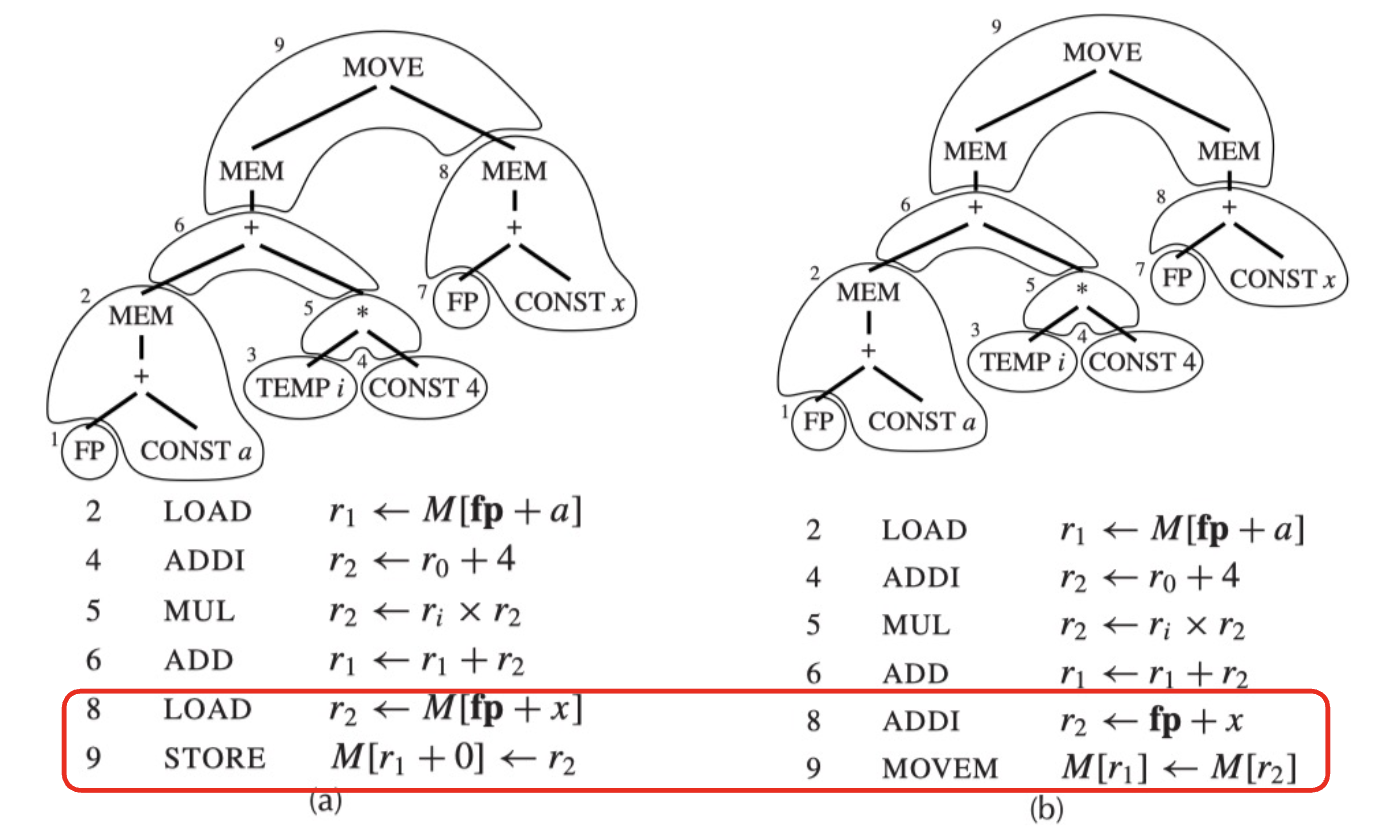
image.png

需要注意的是，一个 IR Tree 可以有多种 tiling 方式。

  • Best Tiling：最少的 cost
    • 对于固定 latency 的机器来说，就是最少的指令数
  • Optimum Tiling：总 tilings 数量最少
    • 全局最优
  • Optimal Tiling：没有任意两个 tiling 能够合并成一个 cost 更小的 tiling
    • 局部最优
  • 每个 optimum tiling 都是 optimal 的，但不是每个 optimal tiling 都是 optimum 的。

2. 选择算法 1：Maximal Munch

假设瓦片越大越好，那么 maximal munch 就是一个贪心算法

  • 从 IR 树根开始往下 top-down
  • 选择能 cover 当前树形的最大瓦片
    • 这里的“最大”定义为节点数最多的瓦片
    • 如果有两个瓦片大小相同，则选择是不确定的/任意的
  • 对子节点重复上述操作
  • 指令生成按照原来的逆序

3. 选择算法 2：Dynamic Programming

前面提到的 Maximum Munch 算法是贪心的，可能会导致 suboptimal 的结果，也就是说这种方法总是找到 optimal 的 tiling，但不一定是 optimum 的。

动态规划算法通过子问题最优能够得到 optimum 的 tiling。

  • 工作方式是 bottom-up
  • 为树的每一个节点赋一个 cost 值
  • 节点 x 的 cost（记作 f(x)）是能够 cover 以 x 为根节点的子树的 best tiling 的 cost
    • \(f(x) = \min_{\forall \ \text{tile}\ t \ \text{covering}\ x} (c_t + \sum_{\forall\ \text{leaf}\ i\ \text{of}\ t}f(i))\)
    • 其中 \(c_t\) 是瓦片 t 的 cost

实现细节：

  • 给出根节点 n，首先寻找好 n 的所有后继节点的 cost（递归地计算）
  • 接着，每个树形（瓦片）会匹配到一个 cost
  • 每个瓦片有零或多个 leaves，上面可以挂载子树
  • 对于每个瓦片 t，其被匹配后的 cost 是 \(c_t + \sum_{\forall\ \text{leaf}\ i\ \text{of}\ t}f(i)\)
  • 选择 cost 最小的树形
例子

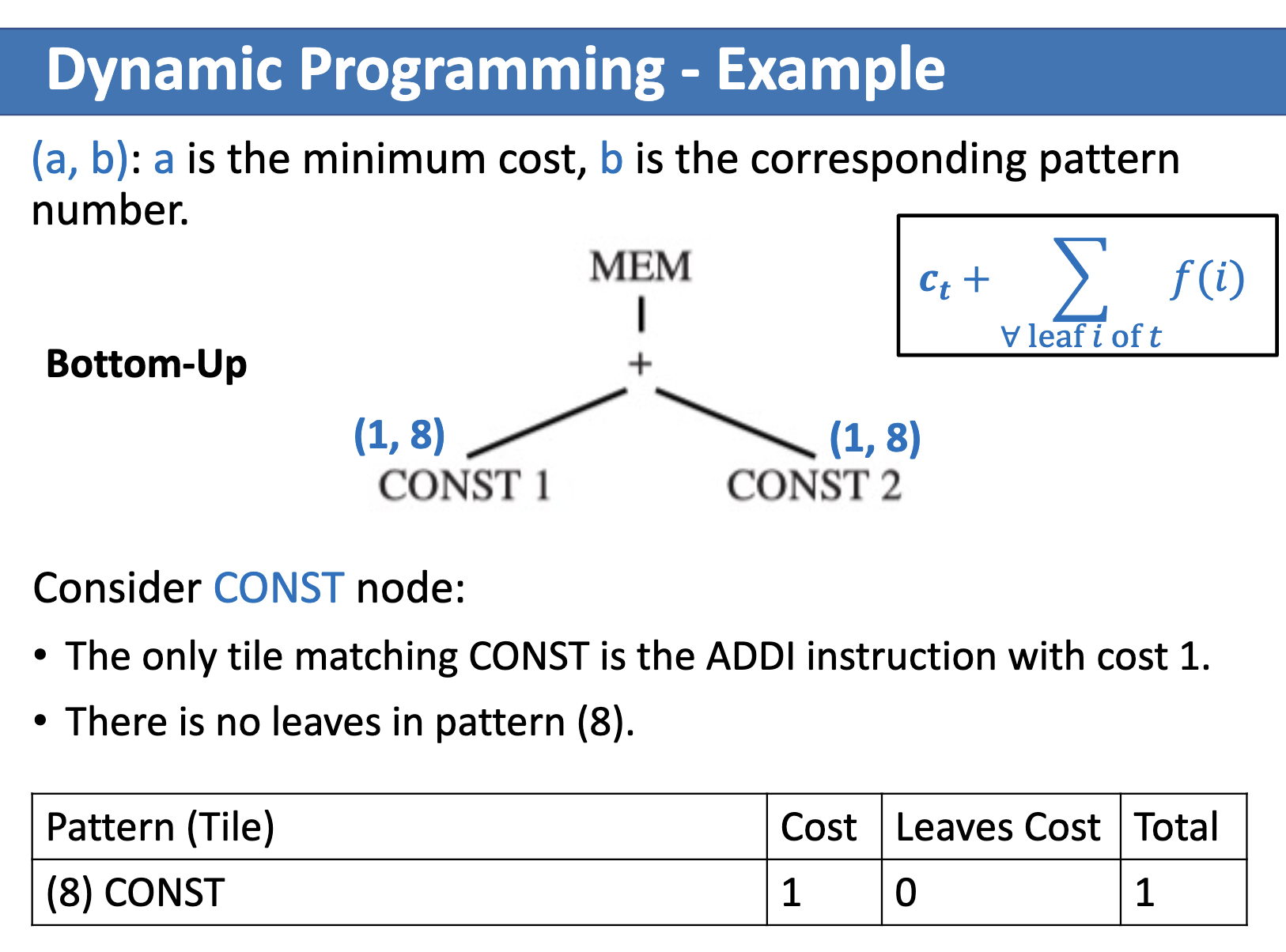
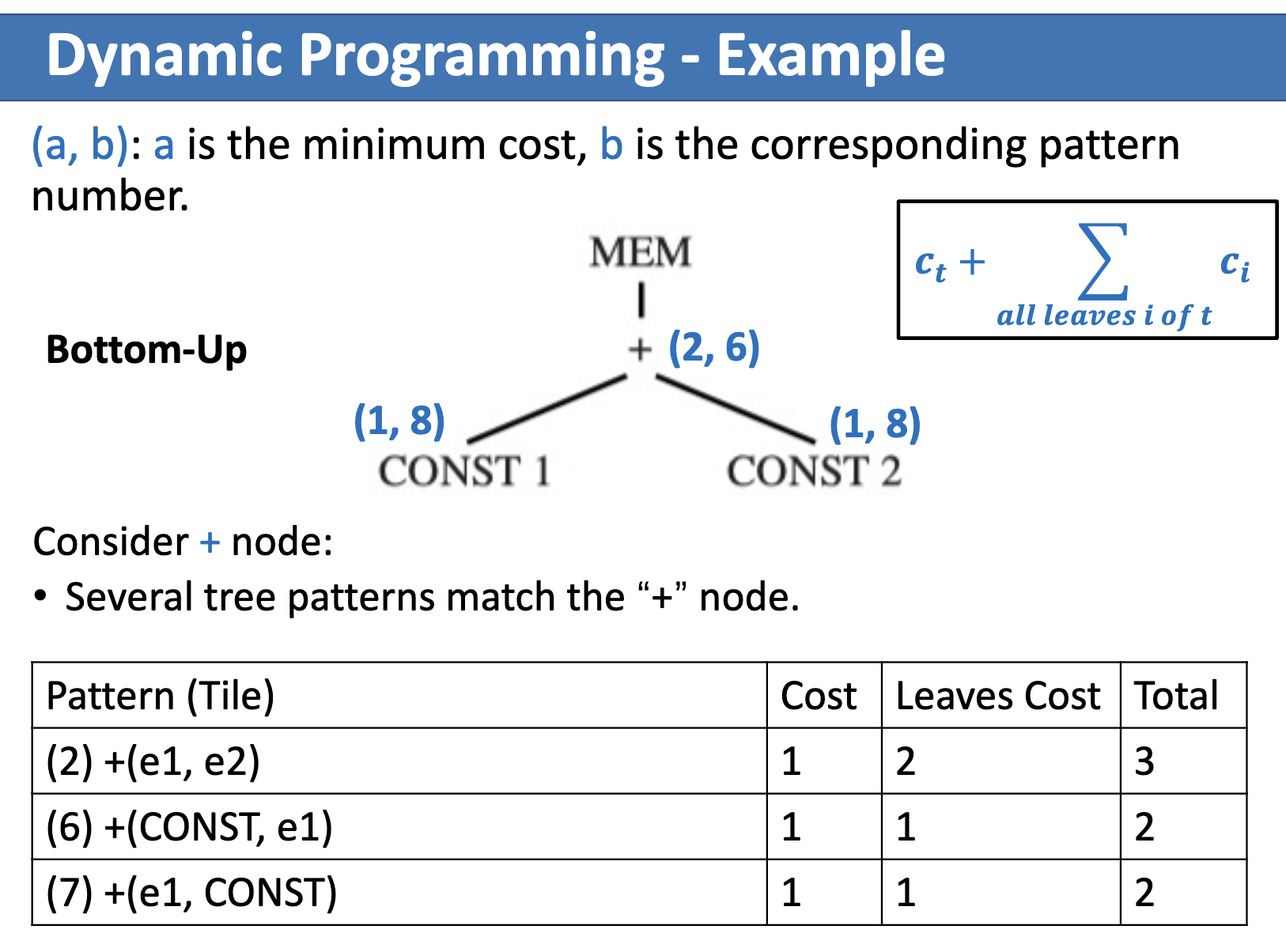
image.png

image.png

image.png

一旦根节点的 cost 被找到，就开始了 instruction emission 的过程：

  • 对节点 n 的每个 leaf li，Emission(li) 会被调用
  • 然后再 emit 节点 n 匹配到的指令

两种算法的效率比较

假设：

  • K：平均每个瓦片有 K 个 non-leaf 节点
  • N：输入 IR 树的节点数量
  • K'：给定一个子树，最多需要检查多少个 node 能够找到对应的瓦片
  • T'：每个 node 平均有多少个可以匹配的瓦片

则：

  • Maximal Munch 的时间正比于 \((K' + T')N/K\)
  • Dynamic Programming 的时间正比于 \((K' + T')N\)
  • 其中 K, K' 和 T' 都是常数，因此二者都是线性的时间
选择算法 3

Tree Grammar。这里先不展开。

4. CISC 指令集

先上一张对比图：

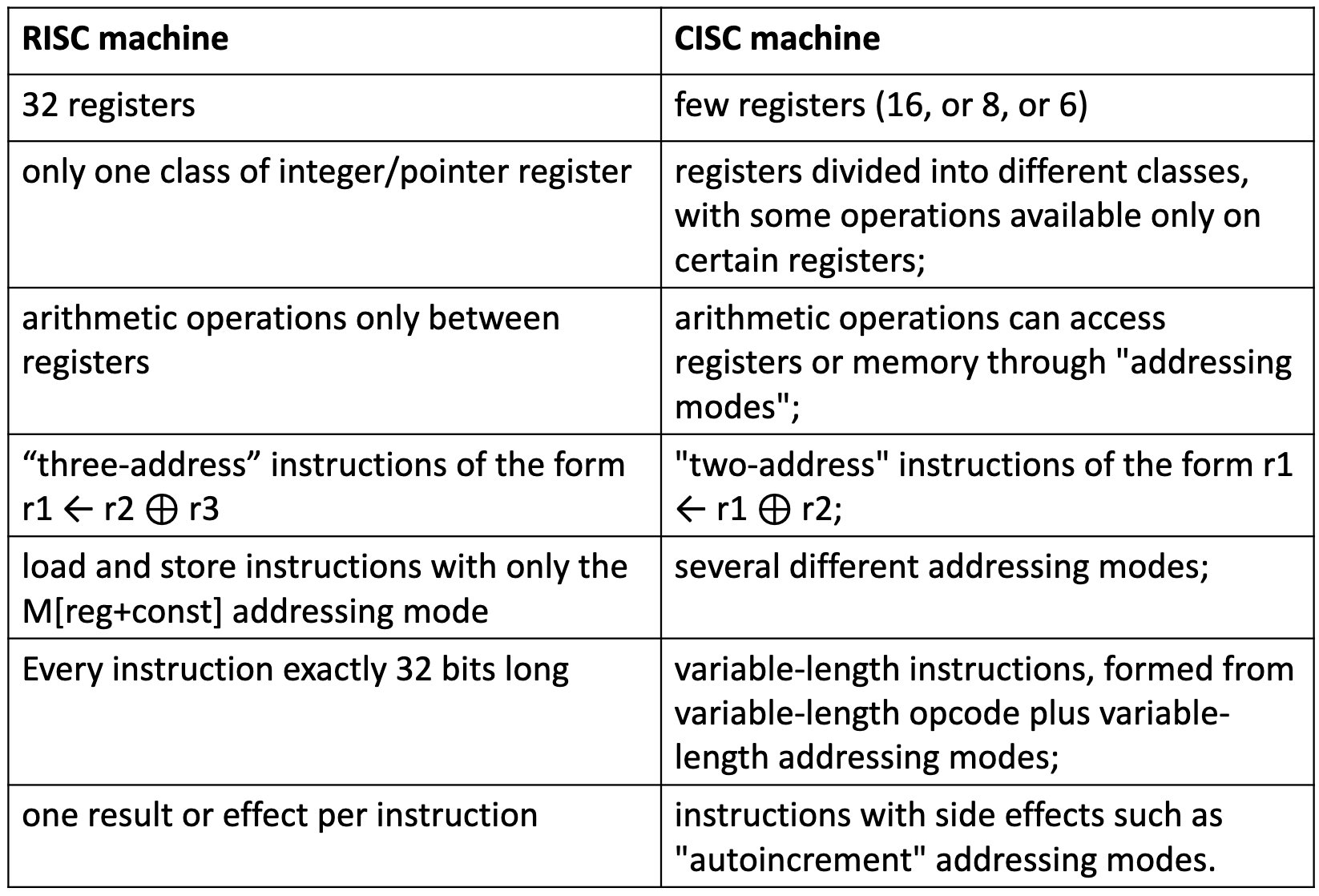
image.png

CISC 指令集相对于 RISC 来说有一些特殊限制，需要单独处理。这里也不多说了。