Abstract Syntax：抽象语法

约 742 个字 33 行代码 1 张图片 预计阅读时间 3 分钟

1. 语义动作（Semantic Actions）

【语法分析】过程传递给【语义分析】过程的数据是抽象语法树（AST）。AST 的创建是通过语法分析中的语义动作来完成的，可以存在于：

• 递归下降分析器中
• Yacc 生成的分析器中

1.1 递归下降中的语义动作

在前面的课程中，已经看到了递归下降的操作流程。例如对于 F -> id, F -> num, F -> (E)，其语法分析过程可以这样写：

void F(void) {
    switch (tok) {
        case ID: { advance(); break; }
        case NUM: { advance(); break; }
        case LPAREN: { eat(LPAREN); E();
            eatOrSkipTo(RPAREN, F_follow); break; }
        case EOF:
        default: printf(“expected ID, NUM, or left-paren”);
                skipto(F_follow);
    }
}

那么现在如果我们想在做语法分析的同时去检验输入并构建 AST，我们可以在每个分支中添加一些代码来实现。比如：

int F(void) {
    switch (tok) {
        case ID: { int i=lookup(tokval.id); advance(); return i;}
        case NUM: { int i=tokval.num; advance(); return i; }
        case LPAREN: { eat(LPAREN); int i = E();
                eatOrSkipTo(RPAREN, F_follow); return i;}
        case EOF:
        default: printf("expected ID, NUM, or left-paren");
                skipto(F_follow);
                return 0;
    }
}

注意到这个时候，F() 函数的返回值类型从 void 变成了 int，这意味着它现在返回一个整数值，这个整数值可以是一个变量的索引或一个数字的值。

也就是说，在递归下降分析器中，语义动作是通过语义分析函数的返回值或函数的副作用（或两者）来实现的。为每一个终结符或非终结符，我们都会绑定一个语义值类型。

一种特殊情形

对于语法规则 T -> T * F，我们可以使用

int T(void) {
    int i = T();
    eat(TIMES);
    int j = F();
    return i * j;
}

这种方式来实现语义动作。这里的 T() 函数调用是递归的，表示在处理乘法时需要先处理左侧的 T，然后处理右侧的 F。

问题来了：之前第三章讲过消除左递归，所以这里的四则运算实际上需要改写为：

E' -> + T E'
E' -> - T E'
T' -> * F T'
T' -> / F T'

这里，只有 right operator，如何设计语法动作呢？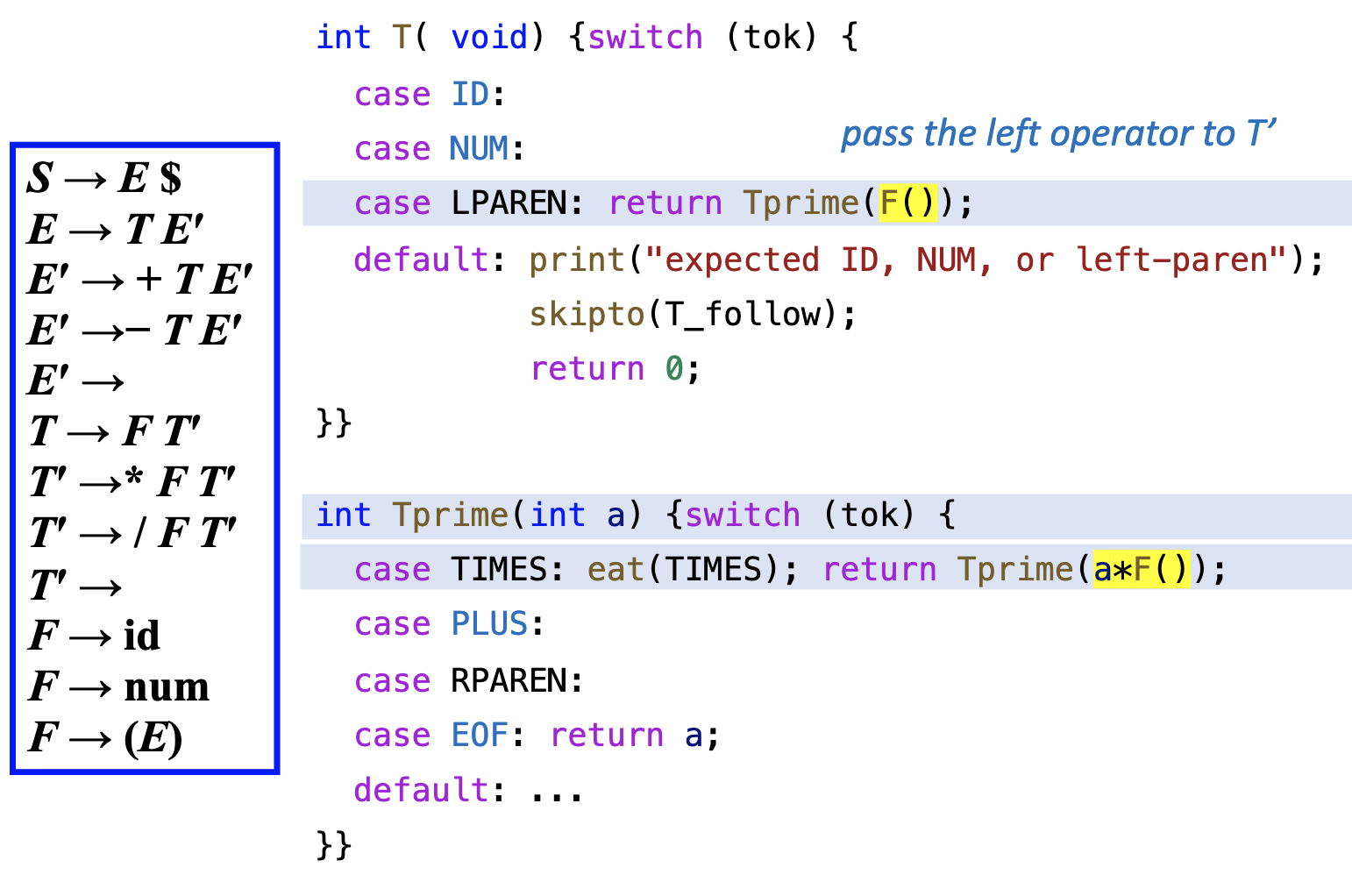

1.2 Yacc 中的语义动作

这部分内容在实验中已经涉及到，且在前面第三章也已经讲过了，这里不再赘述。

每一个符号都绑定了语义值，维护符号栈的时候也维护了值栈，当分析器做 reduction 的时候，就对栈进行 pop + push 操作。

2. 抽象语法树（AST）

抽象语法树（AST）是一个树形结构，用于表示源代码的语法结构。它是从源代码中提取的抽象表示，去除了具体的语法细节，保留了程序的逻辑结构。

具体细节在实验中已经涉及到，这里不再赘述。

需要注意的是，有时候可能需要语法分析器能够报出错误发生的位置，这需要词法分析器和语法分析器之间的协作。通常，词法分析器会在每个 token 中包含位置信息（如行号和列号），而语法分析器可以利用这些信息来报告错误。语法分析器应该维护一个 position stack，记录每个 token 的位置信息，以便在发生错误时能够准确地报告错误位置。（Bison 可以自动处理这个问题，而 Yacc 不行）